Oft besteht bei der Verarbeitung von Messsignalen die Situation, dass die relevanten Daten in einem Messsignal zwar vorhanden sind, eine direkte Interpretation aber nur schwer oder gar nicht möglich ist. Hier kommen geeignete Transformationen des Eingangssignals ins Spiel.
Messsignalverarbeitung – ein kleines praktisches Beispiel
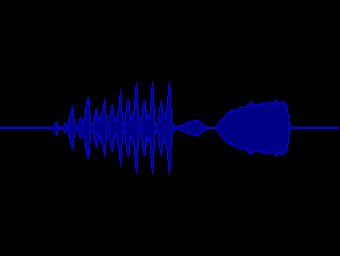
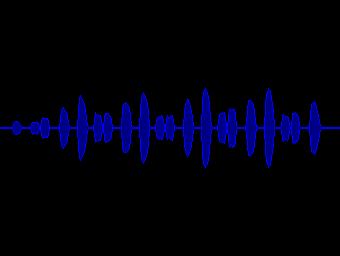
Ein akustisches Messgerät erhält Daten von einem Mikrofon und soll nun ein Steuerungssignal auslösen, wenn der Ruf einer Goldammer ertönt und beim Ruf der Kohlmeise soll ein anderes Steuersignal geschaltet werden. Nun stellt sich die Frage, wie löst man diese Aufgabe? Der Computer hat keine Ohren und die alleinige Interpretation der Audiosamples führt hier nicht wirklich weiter.
Wie kann der Computer den typischen Ruf der Goldammer (si-si-si-si-si-si zii-düüh) vom Klang des Rufs der Kohlmeise unterscheiden? Die Lösung liegt in der Transformation.
Die Ausgangssituation:
Für uns Menschen sieht das erst einmal einfach aus. Problematisch wird es spätestens für uns Menschen bei 10 bis 100 verschiedenen Vogelarten, die zu unterscheiden sind.
Für den Computer ist die Betrachtung des Audiosignals problematisch. Erstens sind es zu viele Daten, bei einer Sampling Rate von 32 kHz und einer Signaldauer von 5 Sekunden muss der Computer bereits einen Vektor von 160.000 Messpunkten analysieren. Zweitens geben die aufeinanderfolgenden Messpunkte zunächst keinerlei Hinweis darüber, welche Frequenzanteile (Tonhöhen, Tonfolgen) das Signal hat.
Also was tun?
Das Lösungswort heißt: TRANSFORMATION
Wir müssen die Daten zunächst in geeigneter Form umwandeln, um sie dann „anders“ und „einfacher“ betrachten zu können.
Folgender Weg führt zum Ziel:
- Transformation des Audiosignals über FFT (Fouriertransformation) in ein Audiospektrum
- Bewertung des Audiospektrums: Reduktion der Frequenzbänder, Abbildung auf MEL-Scala
- Weitere Datenreduktion der logarithmischen MEL Scala und Dekorrelation, das liefert uns die MFCC (Mel Frequency Cepstral Coefficients)
- Zusammenfassung aufeinanderfolgender Audiospektren (einzelne MFCC Vektoren) zu einer Matrix
- Konvertierung dieser Matrix über eine geeignete Farbskala (ColorMap) in ein Bild (Image)
- Jetzt haben wir die Brücke geschlagen zur Bildverarbeitung / Bilderkennung.
- Wir haben es geschafft, unsere Vogelstimmen in ein geeignetes Bild zu transformieren.
- Nutzung eines KI-Frameworks (künstliche Intelligenz) zur Bewertung / Erkennung der Bilder.
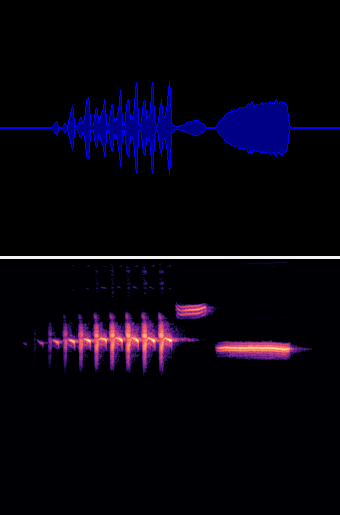
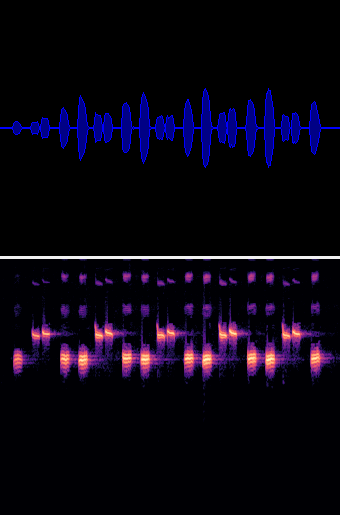
Im Endergebnis haben wir nun folgendes Bild:
Das Audiosignal mit 32 kHz Sample Rate wurde blockweise via FFT (4096) in einzelne Audiospektren zerlegt. Jeder Block ist in diesem Beispiel jetzt 10 ms lang, also 320 Samples.
Aus den entstandenen 2048 FFT Spektrallinien wird eine logarithmische MEL-Skala der Länge 256 gebildet.
Jeder einzelne MEL Block (256) entspricht jetzt einer vertikalen Spalte in der oberen Grafik.
Bereits jetzt könnte man eine KI-Analyse auf die entstanden Spektralbilder anwenden und würde brauchbare Ergebnisse für die Stimmenerkennung erhalten.
Was in der Praxis als weiterer Verarbeitungsschritt noch folgt – und in diesem Beispiel weggelassen wurde – ist ein weiterer Transformationsschritt, eine Dekorrelation. Aus den MEL-Vektoren werden Koeffizienten berechnet, die MFCC (Mel Frequency Cepstral Coefficients). Dies führt zu einer nochmaligen Datenreduktion und entspricht mathematisch einer Dekorrelation.
Typisch wäre für diesen Anwendungsfall jetzt beispielsweise eine MFCC-40 bis MFCC-64 zu rechnen, also 40 bis 64 Koeffizienten. Im einfachsten Fall erledigt das eine Diskrete Kosinus-Transformation. Die DCT führt eine Dekorrelation der logarithmierten MEL Spektren aus. Die entstehenden MFCC (Koeffizienten) repräsentieren dann das Audiosignal in dekorrelierter Form.